Juegos y Acertijos MENSA (Nivel Medio II)
Recopilación de Juegos y Acertijos MENSA gratuitos para realizar online
1.- AREA DE UNA SUPERFICIE EMBALDOSADA
Supongamos una superficie de baldosas cuadradas de un metro de lado, sobre ella dibujamos un polígono tan caprichoso como nos apetezca (ver la figura) formado por líneas rectas que unen exclusivamente vértices de las baldosas. Llamaremos N al número de los vértices que estén sobre la línea perimetral y B al número de vértices interiores al polígono. Se trata de encontrar una fórmula que en función de N y B, proporcione el valor de la superficie del polígono.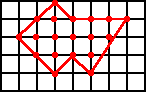
SOLUCIÓN
S=(N’-2)/2 , siendo N’=(N+2B).
Esto resulta obvio para la figura formada por sólo dos puntos en vértices consecutivos, cuya área es cero. Por cada punto adicional que añadamos en la periferia inmediata, aumenta el área en media unidad, quedando de este modo demostrada por inducción la fórmula.
2.- ¿CÓMO CORTAR EL QUESO?
Los aficionados al queso de Camembert saben que este suele presentarse en piezas discoidales. Saben también que suele cortarse en sectores para su consumo, y que al dejar parte del queso cortado y sin consumir,la zona del del corte se seca y pierde su delicioso sabor.
Procede pues, si no vamos a terminar en un día todo el disco de queso, cortarlo de la forma más eficaz posible para evitar pérdidas. Centraremos nuestra atención en el caso de que deseemos hace porciones del mismo tamaño.
El problema, matemáticamente, se planteará así:
Dado un círculo de radio unidad, ¿cómo dividirlo en n partes de la misma área de forma que el perímetro fronterizo sea de la menor longitud posible?
SOLUCIÓN
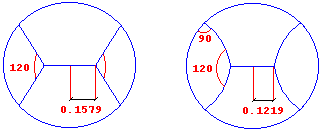
Pero para n=4 la cosa comienza ya a complicarse. Pues un corte según cuatro sectores de noventa grados arrojaría una longitud de corte L=4, mientras que en el sistema indicado en la figura de la izquierda basta con L=3,9624.
Esta división se ha obtenido recordando la conocida propiedad de que el punto situado en el interior de un triángulo cuya suma de distancias a los tres vértices es mínima es el que ve estos bajo ángulos de 120 grados. Sin embargo, todavía puede mejorarse: intuitivamente se comprende que, al no ser los segmentos rectos incidentes sobre la circunferencia perpendiculares a ésta podrían ser sustituídos por arcos de circunferencia que cumplieran con esta condición. Se mejora todavía algo, llegando a la figura de la derecha donde L=3,9412.
3.- LA RULETA RUSA 2.0
El cine ha popularizado el macabro juego de la ruleta rusa. Los dos jugadores están provistos de un único revólver de seis tiros cargado con una única bala, y cada uno, alternativamente, gira un paso el cilindro y dispara una vez apuntando a su propia sien.
Si el juego se repite tres veces por jugador, la muerte de uno de ellos es segura, y cada uno tiene la misma posibilidad de ser elegido, el 50 %.
Existen variantes más atenuadas, que dan una esperanza de supervivencia. Una de ellas es que cada jugador, al recoger el revólver de las manos del otro, antes de efectuar su disparo gira el cilindro al azar. Pero en este caso el segundo jugador tiene ventaja. Si cada uno aprieta tres veces el gatillo, las respectivas posibilidades de morir son:
Jugador 1: p1 = 0.363
Jugador 2: p2 = 0.302
¿Puede compensarse algo este desequilibrio? Existen varios medios. Uno de ellos es que el segundo jugador apriete el gatillo sus dos primeras veces de forma seguida. Con ello las probabilidades respectivas son:
Jugador 1: p1 = 0.330
Jugador 2: p2 = 0.335
Demuéstrese.
SOLUCIÓN
Primer jugador, primer disparo : p11 = 1/6 = 0,167
Segundo jugador, primer disparo : p21 = (1 – p11)1/6 = 0,139
Segundo jugador, segundo disparo : p22 = (1-p11-p21)1/6 = 0,116
Primer jugador, segundo disparo : p12 = (1-p11-p21-p22)1/6 = 0,096
Segundo jugador, tercer disparo : p23 = (1-p11-p21-p22-p12)1/6 = 0,080
Primer jugador, tercer disparo : p13 = (1-p11-p21-p22-p12-p23)1/6 = 0,067
La suma de las respectivas probabilidades es:
p1 = p11 + p12 + p13 = 0,330
p2 = p21 + p22 + p23 = 0,335
4.- EL CASTILLO ENCANTADO
Querido amigo: Al poco tiempo de comprar esta vieja mansión, tuve la desagradable sorpresa de comprobar que está hechizada con dos sonidos de ultratumba, que la hacen prácticamente inhabitable: un canto picaresco y una risa sardónica.
Aún conservo, sin embargo, cierta esperanza, pues la experiencia me ha demostrado que su comportamiento obedece ciertas leyes oscuras, pero infalibles, y que puede modificarse tocando el órgano y quemando incienso.
En cada minuto, cada sonido está presente o ausente: lo que cada uno de ellos hará en el minuto siguiente depende de lo que pasa en el minuto actual de la siguiente manera:
El canto conservará el mismo estado (presente o ausente), salvo si durante el minuto actual no se oye la risa y toco el órgano, en cuyo caso el canto toma el estado opuesto.
En cuanto a la risa, si no quemo incienso, se oirá o no según que el canto esté presente o ausente (de modo que la risa imita al canto con un miuto de retraso). Ahora bien, si quemo incienso, la risa hará justamente lo contrario de lo que hacía el canto.
En el momento en que le escribo, estoy oyendo a la vez la risa y el canto. Le quedaré muy agradecido si me dice que manipulaciones de órgano e incienso debo seguir para restablecer la calma.
SOLUCIÓN
Las condiciones pueden resumirse así:
A – SI NO(RISA) Y ORGANO -> CANTO CAMBIA
B – En cualquier otro caso CANTO NO CAMBIA
C – SI INCIENSO -> RISA hará lo contrario que canto
D – SI NO(INCIENSO), la risa hará lo mismo que el canto
|
Minuto |
1 |
2 |
3 |
4 |
5 |
|
RISA |
SI |
NO |
NO |
NO |
NO |
|
CANTO |
SI |
SI |
NO |
NO |
NO |
|
INCIENSO |
SI |
SI |
NO |
NO |
|
|
ORGANO |
SI/NO |
SI |
NO |
NO |
|
Al quemar incienso en el minuto 1, en el 2 la risa no se oirá (por C).
En el minuto 2, el canto se oirá, tanto si el órgano suena como sin no (por A y B).
Al quemar incienso en el minuto 2, en el 3 la risa no se oirá (por C).
Al sonar el órgano en el minuto 2, en el 3 el canto no se oirá (por A).
Al no quemar incienso en el minuto 3, en el 4 la risa no se oirá (por D).
Al no tocar el órgano en el minuto 3, en el 4 el canto no se oirá (por B).
Por consiguiente, las manipulaciones que haremos serán: en el primer minuto quemar incienso; en le segundo minuto quemar incienso y tocar el órgano, a partir del tercer minuto dejaremos de tocar el órgano y quemar incienso y la calma será eterna …
Se toma una baraja española y se preparan tres hojas de papel que llamaremos A,B y C. Se coloca la baraja en A, se toma una carta al azar y tras verla se coloca en C.
A continuación se pasan del grupo A al B tantas cartas como faltan desde el punto de la vista a 12 (si la vista es un as, se pasan 11, si es un rey, ninguna).
Se repite este proceso tantas veces como sea posible; de este modo se llega a un paso en que se agota exactamente el montón A, o faltan cartas. Si faltan se pasan de B a A las que sean necesarias para completar el complemento a 12 de la última colocada en C.
Sabiendo el número de cartas que hay en cada uno de los montones, deducir la suma de las cartas del grupo C.
Generalizar el juego para cualquier número de cartas iniciales y cualquier valor a completar en el trasvase de A a B descrito.
SOLUCIÓN
• El número de cartas traspasadas de montón para completar los puntos de las cartas que se echan al montón C es 2Na + Nb.
• El valor de una carta que se echa al montón C más las cartas traspasadas por ella suman el punto a conseguir P.
Por tanto, el sumatorio de los puntos de las cartas del montón C vale: PNc – (2Na + Nb)
Nota: Los problemas y acertijos se han obtenido de fuentes libres de internet y/o de publicaciones ya extintas.