Juegos y Acertijos MENSA (Nivel Medio I)

Recopilación de Juegos y Acertijos MENSA gratuitos para realizar online

1.- LA RULETA RUSA

Seis individuos deciden jugar a la ruleta rusa con un revólver de seis tiros con una bala. Con las posiciones decididas, el último sugiere que, tras cada intento, en lugar de seguir con el cilindro avanzado una posición, se gire éste aleatoriamente.

¿Cómo mejora esto sus posibilidades?

SOLUCIÓN
En la ruleta rusa habitual su probabilidad de muerte es 1/6 = 0,167. Con el artificio propuesto, la probabilidad de que el revólver no haya disparado todavía a la n-sima vez es: p1 = (5/6)n

El sexto jugador sucumbirá si el revólver se dispara la vez sexta, duodécima, etc.
Es decir:
p = (1/6)[(5/6)5 + (5/6)11 + …] = 55/(66-56) = 0,101

2.- DOS NÚMEROS CONSECUTIVOS EN LA LOTERÍA PRIMITIVA

 
Determinar la probabilidad de que en un sorteo de Lotería Primitiva aparezcan al menos dos números consecutivos cualesquiera.

 

SOLUCIÓN
La solución más sencilla pasa por calcular el número de combinaciones en las que no hay números consecutivos y restarlo luego del total.

Consideremos los dos conjuntos siguientes:

C1 = Combinaciones de 6 números del 1 al 49 tales que entre ellos no hay dos consecutivos.

C2 = Combinaciones cualesquiera de números del 1 al 44.

Ambos conjuntos tienen igual número de elementos, dado que existe entre ellos la siguiente correspondencia biunívoca: (a,b,c,d,e,f) <-> (a,b-1,c-2,d-3,e-4,f-5)

dónde a,b,c,d,e,f son números entre 1 y 49 tales que no hay entre ellos dos consecutivos. Por ejemplo, la combinación (1,5,7,20,35,49) de C1 se correspondería con la (1,4,5,17,31,44) de C2. El número de C2 es el combinacional de 44 sobre 6 = 7.059.052. Puesto que C1 y C2 tienen el mismo número de elementos Card(C1)=Card(C2)=7.059.052.

La cantidad total de combinaciones de la Lotería Primitiva es el combinacional de 49 sobre 6 = 13.983.816.

Luego, el número de tales combinaciones en las que no hay dos elementos consecutivos es la diferencia: 13.983.816 – 7.059.052 = 6.924.764

La probabilidad de que salgan dos números consecutivos cualesquiera en un sorteo es, en consecuencia 49,52%.

3.- EL SUPERCLÁSICO DE MENSA

Este sencillo juego de ingenio, apareció durante muchos años en los periódicos del Reino Unido acompañando a un anuncio de Mensa.

¿Puede usted resolver este problema tan rápidamente como Einstein?

SOLUCIÓN
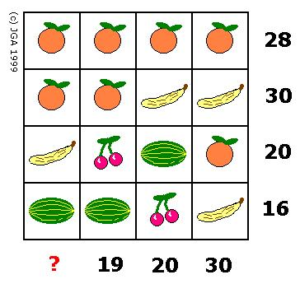
Representamos la naranja por n, el plátano por p, las cerezas por c y el melón por m.

i) 4 x n = 28
ii) 2 x n + 2 x p = 30
iii) p + c + m + n = 20
iv) 2 m + c + p = 16

De i) obtenemos que n=7, de ii) que p = 8 y de iii) y iv) que m=3 y c = 2.

Luego la suma de la columna incógnita vale 25.

4.- PELIGROS DE LA INTUICIÓN

Se tienen cuatro dados cuyas caras están numeradas como sigue:

A

B

C

D

5

4

3

2

5

4

3

2

5

4

3

2

1

4

3

2

1

0

3

6

1

0

3

6

 

Dos jugadores escogen un dado cada uno. Echan los dados y el que obtiene el número más bajo paga una peseta al otro. Un estudio de los datos permite comprobar que:

• El dado A gana al B en 24 de cada 36 tiradas.
• El dado B gana al C en 24 de cada 36 tiradas.
• El dado C gana al D en 24 de cada 36 tiradas.

Se puede establecer un orden de mejor a peor, que es:

A mejor que B mejor que C mejor que D. El jugador que escoge en primer lugar tiene, pues, una ventaja que, para que el juego sea equitativo, debe compensar con un pago inicial. Si prevé jugar 36 partidas, ¿cuál ha de ser este pago?

SOLUCIÓN
El problema es ilusorio. Basta con comparar y se comprobará que el dado D gana también al A en 24 de cada 36 ocasiones. La asunción implícita de que el concepto mejor que es transitivo debe descartarse.

Un análisis más a fondo demuestra que la simetría entre los dados dos a dos no se extiende al total. El dado A que, según hemos visto, gana al B y pierde con el D, empata con el C. El dado B, que pierde con el A y gana al C, pierde por poco con el D.

Si se echaran simultáneamente los 4 dados, no ganarían todos por igual en las 1296 combinaciones posibles:

• A gana 432 veces.
• B gana 288 veces.
• C gana 144 veces.
• D gana 432 veces.
•

Es decir, son mejores los dados A y D, peor el B y mucho peor el C. Si la competencia fuese entre tres, los resultados serían similares:

• ABC: A=108, B=72, C=36
• ABC: A=72, B=48, C=96
• ACD: A=72, C=72, D=72 (Único caso simétrico)
• BCD: B=96, C=48, D=72

5.- UNO GEOMÉTRICO SENCILLO

Imaginemos un cubo de lado L. Tomemos dos vértices opuestos por una diagonal máxima del cubo que mide (3)1/2 L. Cada uno de estos dos vértices opuestos está rodeado de tres vértices cercanos que forman un triángulo. Es fácil ver que los dos planos definidos por estos dos triágulos son paralelos. La cuestión es hallar, sin hacer cálculos, cuál es la distancia entre los dos planos.

SOLUCIÓN
La diagonal es perpendicular a los planos en cuestión y forma ángulos iguales con todas las aristas del cubo, por lo que la proyección de una cualquiera de éstas sobre aquélla es constante. Luego, sin más que dibujar la figura, se concluye que la distancia entre los dos planos es 1/3 de la diagonal.

Nota: Los problemas y acertijos se han obtenido de fuentes libres de internet y/o de publicaciones ya extintas.