Juegos y Acertijos MENSA (Nivel Fácil IV)
Recopilación de Juegos y Acertijos MENSA gratuitos para realizar online
1.- EL MONJE BUDISTA VIAJERO
Una mañana, exactamente al amanecer, un monje budista emprendió la ascensión de una elevada montaña. El sendero que utilizó, de no más de un metro de ancho, daba vueltas y revueltas en torno a la montaña, hasta un resplandeciente cerro en la cima. El monje fue subiendo con velocidad variable, deteniéndose muchas veces a descansar y a comer frutos secos que llevaba consigo. Alcanzó el templo poco antes de la puesta del sol. Tras varios días de ayuno y meditación, emprendió el viaje de regreso a lo largo del mismo sendero, partiendo al amanecer, caminando igualmente con velocidad variable y haciendo muchas pausas a lo largo del camino. Su velocidad media en el descenso fue, como era de esperar mayor que en el ascenso. Demuéstrese que hay un punto del camino por el que el monje pasó en ambos viajes a la misma hora del día.
SOLUCIÓN
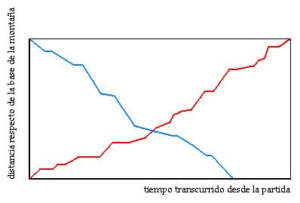
La figura representa la distancia a la que se encuentra el monje de la base de la montaña en función del tiempo. El camino de ida se ha representado en rojo y el de vuelta en azul. Como el enunciado dice que en el camino de regreso el monje tiene una mayor velocidad, en valor medio, el tiempo transcurrido en recorrer la distancia es menor. Es obvio que las dos líneas se cruzarán en un punto, da igual el trazado que hagamos, y en ese instante del día es cuando el monje pasa por el mismo sitio tanto en el ascenso como en el descenso. Daría igual que la velocidad media del descenso fuese menor que la del ascenso, en ese caso la línea azul cortaría el eje horizontal de la gráfica más hacia la derecha pero también tendría un punto de intersección con la línea roja.
2.- CRIPTOSUMA
Hallar el valor de la cifra que falta.
SOLUCIÓN
Cada ficha lleva en el recuadro inferior el valor de la posición en el alfabeto de la letra que aparece en el recuadro superior multiplicado por 3.
Así A – 3, B – 6, C – 9, D -12, …
3.- LA COMPRA DE NAVIDAD
El señor y la señora Winter han ahorrado para comprar regalos navideños. Al romper la hucha calculan que los regalos de este año no deben costar, en media, más de 60 coronas. Merced a la buena suerte, los Winter encontraron una auténtica ganga: un encantador reno en nylon de color rosa que canta «Jingle Bells». Los Winter creen que el regalo gustará a gran parte de la familia, así que se gastan la mitad de sus ahorros en renos de color rosa. ¿Cuantos regalos más pueden comprar, sabiendo que cada reno cuesta 30 coronas y que cada miembro de la familia recibirá un sólo regalo?
SOLUCIÓN
4.- JUEGO DE VASOS
Moviendo un sólo vaso conseguir que queden en la secuencia:
LLENO-VACÍO-LLENO-VACÍO-LLENO-VACÍO
SOLUCIÓN
Se toma el segundo vaso empezando por la izquierda, se vacía en el quinto vaso y se vuelve a dejar donde estaba.
Se tienen cuatro cartas que se sabe tienen números en una de sus caras y letras en el reverso. Estas cartas están dispuestas sobre la mesa tal como se muestra en la siguiente figura: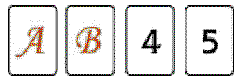
Además, se tiene la siguiente afirmación: “Si una carta tiene un número par en uno de sus lados, entonces tiene una vocal en el otro.”
¿Cuántas cartas hay que dar vuelta para comprobar que dicha afirmación es verdadera?
SOLUCIÓN
Nota del Editor: Tal y como está redactado el enunciado, nada impide que una carta con un número impar tenga una vocal en el reverso. Por tanto, sólo sería necesario comprobar que tras la «B» no hay un número par y que por la otra cara del «4» sí hay una vocal. En mi opinión, y en la de otros lectores de la colección podría solucionarse sin mover la carta con la letra «A».
Nota: Los problemas y acertijos se han obtenido de fuentes libres de internet y/o de publicaciones ya extintas.