Juegos y Acertijos MENSA (Nivel Fácil II)
Recopilación de Juegos y Acertijos MENSA gratuitos para realizar online
1.- EL MONASTERIO
En un monasterio, los monjes sólo se reúnen una vez al día para cenar. El resto del tiempo lo pasan rezando a solas, sin verse. No pueden hablar. El único que puede hablar es el abad.
Un día les dice: «Una terrible enfermedad no contagiosa ha llegado al monasterio y, desgraciadamente, veo que hay monjes infectados. El único síntoma que se puede apreciar es que al enfermo se le pone la cara negra. Sin embargo, él no sentirá nada. Quien contraiga la enfermedad debe suicidarse en cuanto lo sepa».
Los monjes siguen con su vida normal, hasta que 10 días después, al reunirse a cenar, ven que faltan algunos de ellos. Van a sus habitaciones y ven que se han suicidado, y que, además, eran los que tenían la enfermedad. En el monasterio no hay espejos ni objetos reflectantes, por lo que los monjes no han podido verse la cara. Además, los monjes son unos lógicos perfectos, y todos confían plenamente en la lógica de sus compañeros.
¿Cómo supieron los monjes infectados que efectivamente tenían la enfermedad?
¿Cuantos estaban enfermos?
SOLUCIÓN
Se suicidaron 10 monjes en la noche del décimo día.
La explicación es un tanto tediosa por escrito, pero es más o menos así: Si sólo un monje hubiese estado enfermo, cuando el abad les contó acerca de la enfermedad y les confirmó que entre ellos había enfermos, ese único monje enfermo no hubiese visto caras negras, deduciendo que era el enfermo.
Si hubieran sido dos los enfermos, al primer día los hubiesen visto una sola cara negra, pero al no haber un suicidio por la noche, hubieran comprendido que había más de un enfermo, siendo ellos el otro (¿se entiende?).
Así sucesivamente, al décimo día todos comprendían que había por lo menos 10 enfermos. Los que solo veían 9 caras, comprendieron que ellos eran el restante y se suicidaron. Si no hubiesen tenido el valor de hacerlo, al undécimo día todos los demás hubieran pensado que estaban enfermos y se hubieran suicidado.
2.- PREGUNTA INDISCRETA
Preguntan a Ariadna:
—¿Cuántos años tienes?
Y ella contesta:
—Anteayer tenía 19 y el año
próximo cumpliré 22.
¿Es esto posible?.
SOLUCIÓN
3.- EL OBJETO MISTERIOSO
Dadas las tres vistas (alzado, planta y perfil), hallar el cuerpo tridimensional al que pertenecen.
SOLUCIÓN
La solución es la siguiente:
4.- SERIE DE VOCALES
Averiguar que conjunto de vocales completa la serie siguiente:
EUIO, EU, IEA, AE, UIE, AU, UAO, EUO.
SOLUCIÓN
La forma más racional de repartir el tesoro es a partes iguales. A Garfio le es igual pactar con Tuerto que con Patapalo, siempre dejando fuera al tercer socio. Supongamos que está acordando con Tuerto repartir a medias. Patapalo podría reaccionar ofreciéndole, por ejemplo, un 80% y conformándose él con un 20%, lo que dejaría fuera a Tuerto. Para evitarlo, éste puede ofrecer a Patapalo el 25%, dejando fuera a Garfio con todo su gran barco. Las ofertas dos a dos pueden sucederse sin cesar sin alcanzar ningún punto de equilibrio.
Por más vueltas que se le dé, cada uno de los socios es capaz de romper el acuerdo entre los otros dos con ofertas mejores si se presume que va a aquedar fuera de la alianza. Lo más sensato es que, olvidándose de supuestas ventajas, pacten repartir por igual.
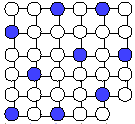
El diagrama indica la ubicación de los 35 barrios de una ciudad. Los círculos son barrios y las líneas carreteras. La distancia entre barrios es 5 Km. El intendente decide que ningún barrio debe estar a más de 5 Km. de un cuartel de bomberos.
¿Cual es la mínima cantidad de cuarteles necesarios?
Indique sus ubicaciones.
SOLUCIÓN
La solución es la siguiente:
Nota: Los problemas y acertijos se han obtenido de fuentes libres de internet y/o de publicaciones ya extintas.